转帖。求康威椭圆的长轴短轴

TSC999

下图中，任意三角形 ABC 边长为 a, b, c。延长 AB、AC 至 A1、A2 使 BA1=CA2=BC=a。对另两边也同样处理如图。证明 A1、A2、B1、B2、C1、C2 共椭圆，此圆叫康威椭圆。康威是英国数学家。
用 a、b、c 及三角形的其他参数（例如面积、外接圆半径、内切圆半径等）来表示康威椭圆的长轴和短轴长度。


注：此问题来源于《数学中国》shuxueren 网友的帖子。此问题尚未解决。康威本人肯定是知道的，但是我们查不到这个资料。

kuing

向量试试手：

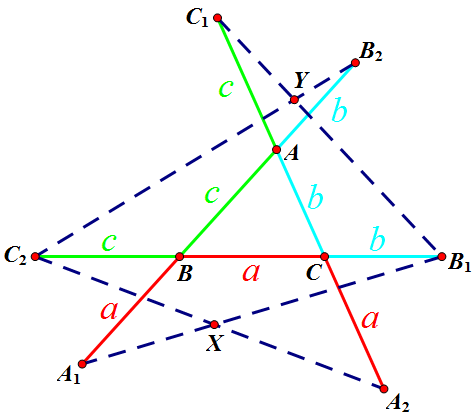
记 `\vv{AB}=\bm x`, `\vv{AC}=\bm y`，则
\begin{align*}
\vv{AA_1}&=\left( 1+\frac ac \right)\bm x, & \vv{AA_2}&=\left( 1+\frac ab \right)\bm y,\\
\vv{AB_2}&=-\frac bc\bm x, & \vv{AC1}&=-\frac cb\bm y,\\
\vv{AB_1}&=-\frac ba\bm x+\left( 1+\frac ba \right)\bm y, & \vv{AC_2}&=\left( 1+\frac ca \right)\bm x-\frac ca\bm y,
\end{align*}设 `A_1B_1` 与 `A_2C_2` 交于 `X`，`C_1B_1` 与 `B_2C_2` 交于 `Y`，利用上述结果可以计算出
\begin{align*}
\vv{AX}&=\frac{(a+b)(a+c)}{a(a^2+ab+ac+2bc)}\bigl( (a-b+c)\bm x+(a+b-c)\bm y \bigr),\\
\vv{AY}&=-\frac{bc}{a(ab+b^2+ac+c^2)}\bigl( (a-b+c)\bm x+(a+b-c)\bm y \bigr),
\end{align*}可见 `X`, `A`, `Y` 三点共线（准确地说 `X`, `Y` 在过 `A` 的周界中线上），于是 `A_1A_2B_1B_2C_1C_2` 六点共二次曲线？……
呃……其实我也不知道“帕斯卡定理”反过来用有没有问题……
不过就算这样也还未能判定是椭圆，更别说要确定它的各种长度……

不知道用“重心坐标”来玩是不是会简单点呢，可惜我也没怎么研究过，有没有六点共椭圆的判定方法之类的……

isee

这个命题好像在哪儿见过，至少半段。。





然后这个名字……突然想起是这位先生

isee

回复 3# isee

原来我以前见到的是 Conway´s Circle
bilibili.com/read/cv10004984/

isee

回复 4# isee

类似命题，六点共椭圆

kuing

回复 5# isee

又有类似命题：zhihu.com/question/459671772

陈九章

上述问题已经被creasson老师解决了。谢谢关注！

hejoseph

并不一定是椭圆，也可能是抛物线或双曲线。用二次曲线的不变量是容易求得轴的长度的，但是计算太麻烦。

hejoseph

令
\begin{align*}
\Delta={}&a^2 b^2 (a^2 - b^2)^2 + a^2 c^2 (a^2 - c^2)^2 +
b^2 c^2 (b^2 - c^2)^2\\
& +
2 a b c (a^5 + b^5 + c^5 - a^2 b^2 (a + b) - a^2 c^2 (a + c) -
    b^2 c^2 (b + c) - a b c (a b + a c + b c))
\end{align*}
则 $\Delta<0$ 时为椭圆，$\Delta=0$ 时为抛物线，$\Delta>0$ 为双曲线。当二次曲线是椭圆或双曲线时，经过坐标轴旋转和平移将方程变为标准方程形式
\[
\frac{x^2}{p}+\frac{y^2}{q}=1
\]
令
\begin{align*}
t&=ab(a+b)+ac(a+c)+bc(b+c)+abc\\
u&=a^3 + b^3 + c^3 - a b (a + b) - a c (a + c) - b c (b + c) + 3 a b c\\
v&=a b (a^4 + b^4) + a c (a^4 + c^4) + b c (b^4 + c^4) -
a b c (a b (a + b) + a c (a + c) + b c (b + c)) -
2 (a^3 b^3 + a^3 c^3 + b^3 c^3)
\end{align*}
$S$ 是 $\triangle ABC$ 的面积，那么
\begin{align*}
p&=\frac{16abc(a+b)(a+c)(b+c)t(2abc\sqrt{abcu}-v)S^2}{(a+b+c)\Delta^2}\\
q&=\frac{16abc(a+b)(a+c)(b+c)t(-2abc\sqrt{abcu}-v)S^2}{(a+b+c)\Delta^2}
\end{align*}
当二次曲线是抛物线时，经过坐标轴旋转和平移将方程变为标准方程形式是
\[
y^2=64S^3\sqrt{-\frac{abc(a+b)(a+c)(b+c)t}{2(a+b+c)v^3}}x
\]

陈九章

这个康威椭圆（5月10日，数学中国论坛›基础数学›康威圆›42楼），
求出了离心率，却求不出长、短半轴长？
creasson老师，也感到很难！

【注】这个只能是椭圆，不可能是抛物线、双曲线！

hejoseph

这个康威椭圆（5月10日，数学中国论坛›基础数学›康威圆›42楼），
求出了离心率，却求不出长、短半轴长？ ...
陈九章 发表于 2021-5-18 22:31

这个简单太多了，直接用仿射变换把 $\triangle ABC$ 变成正三角形就行了。

hejoseph

令
\begin{align*}
\Delta={}&a^2 b^2 (a^2 - b^2)^2 + a^2 c^2 (a^2 - c^2)^2 +
b^2 c^2 (b^2 - c^2)^2\ ...
hejoseph 发表于 2021-5-18 12:40

对椭圆的情形附一个验证的图

陈九章

hejoseph老师的公式，全面而透彻，很好！
但是，我更喜欢creasson老师的公式：
他仅用三个（外接圆、内切圆、康威圆）半径R、r、T，
表达了康威椭圆、双曲线的长短、实虚半轴长

为二位老师点赞！