|
|
果然是阿氏圆.
正方形$OADB$边长为1, 以$D$为圆心作半径为1/2的圆. $C$为$\odot D$上的动点, 求$CA + 2CB$的最小值.
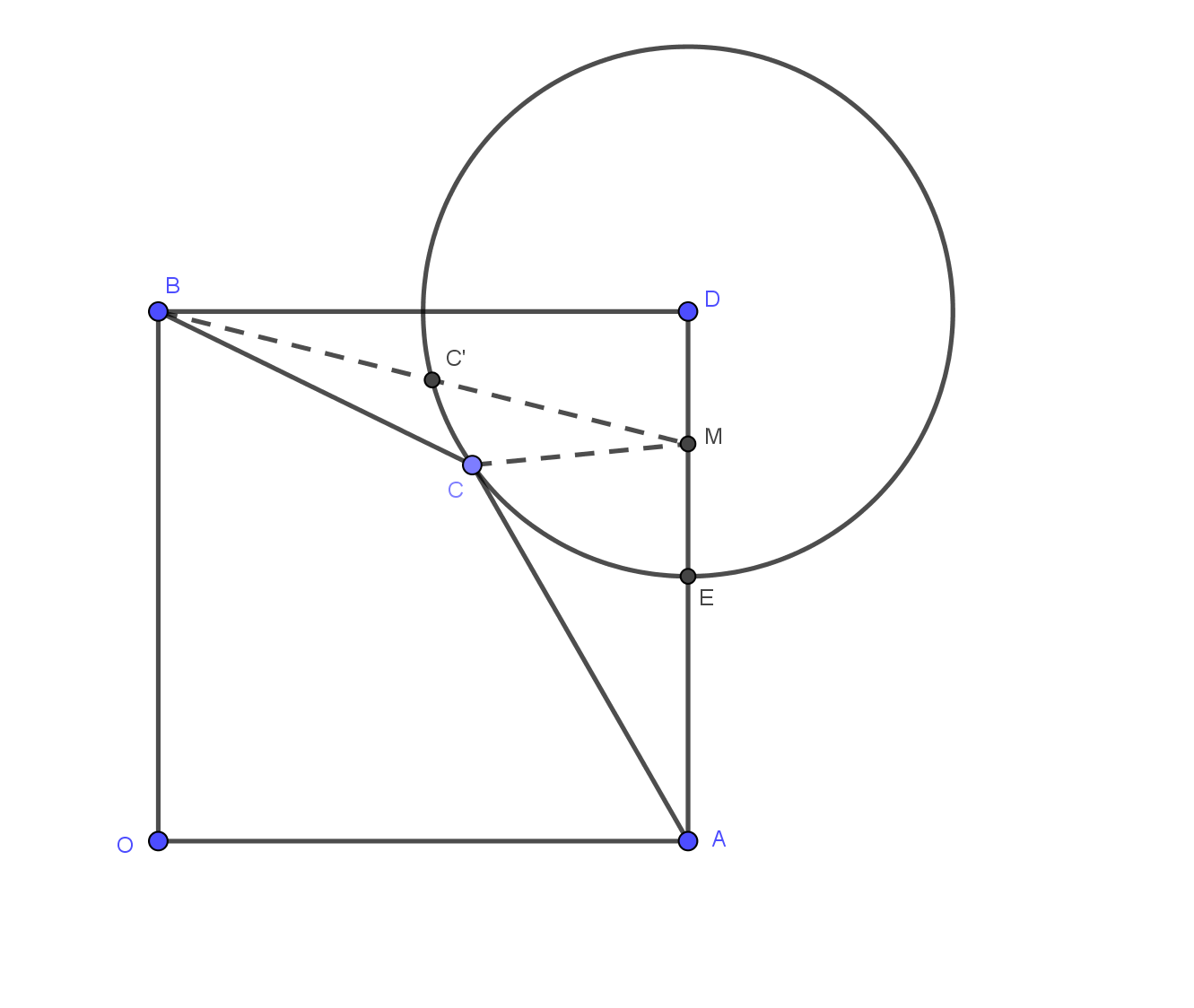
取$DE$中点$M$, 连接$CM$. 可以证明$\odot D$是$\triangle ACM$ 的 $C-$阿氏圆, $\therefore AC = 2CM$.
\begin{equation}
CA+ 2CB = 2CM + 2CB = 2(CM + CB)
\end{equation}
显然当点$C$落在线段$BM$与$\odot D$交点处$C'$时取最小值$2BM=\sqrt{17}/2$
可是最大值好像就只能硬算了, 有人能想出简洁方法吗? |
|