二元函数min(⋯)的最大值

hbghlyj

如何证明$\min\left\{\begin{array}{l}
1 \\
1-\cos (2 x) \\
1+\cos (2 x) \\
1-\cos (2 x-2 y) \\
1+\cos (2 x-2 y) \\
1-\cos (2 y) \\
1+\cos (2 y) \\
1-\sin (2 x) \\
1+\sin (2 x) \\
1-\sin (2 y) \\
1+\sin (2 y) \\
\end{array}\right\}$的最大值为$1 - \frac1{\sqrt2}$ ?

1. f[x_, y_] =
2.   Min[1, 1 - Cos[2 x], 1 + Cos[2 x], 1 - Cos[2 x - 2 y], 1 + Cos[2 x - 2 y],
3.    1 - Cos[2 y], 1 + Cos[2 y], 1 - Sin[2 x], 1 + Sin[2 x], 1 - Sin[2 y],
4.    1 + Sin[2 y]];
5. Maximize[f[x,y],{x,y}]

Copy the Code

Maximize无法找到最大值，因为函数不平滑。
使用NMaximize结果为{0.292893, {x -> -1.1781, y -> -0.392699}}

函数对称性

1. f[x + π/2, y] == f[x, y] // FullSimplify
2. (*    True    *)
4. f[x, y + π/2] == f[x, y] // FullSimplify
5. (*    True    *)
7. f[π/2 - x, π/2 - y] == f[x, y] // FullSimplify
8. (*    True    *)
10. f[y, x] == f[x, y] // FullSimplify
11. (*    True    *)

Copy the Code

画图

Plot3D[f[x, y], {x, -π/2, π/2}, {y, -π/2, π/2}, PlotRange -> All, Exclusions -> None, PlotLegends -> Automatic, PlotPoints -> 100, MaxRecursion -> 5, AxesLabel -> Automatic] Copy the Code
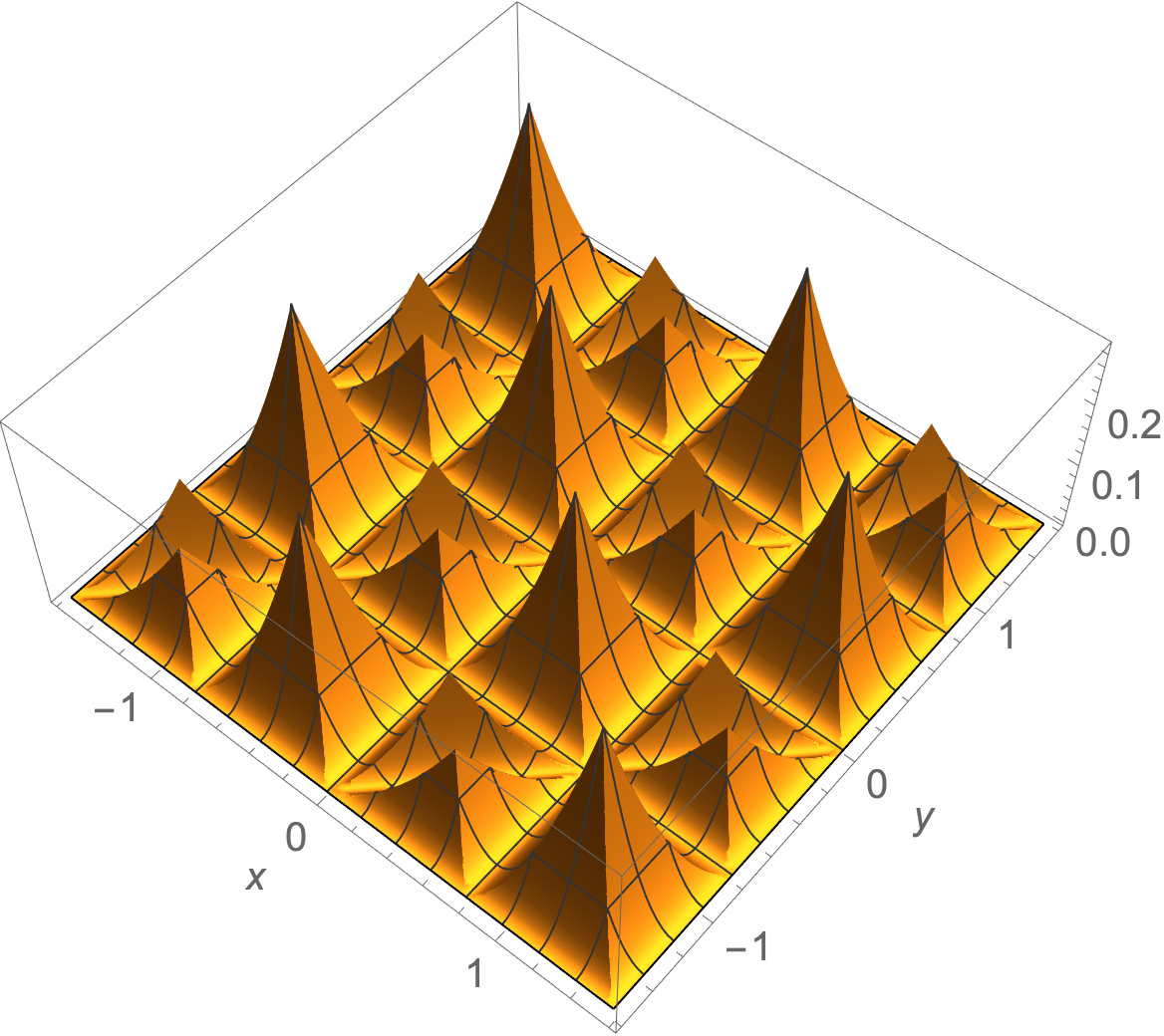
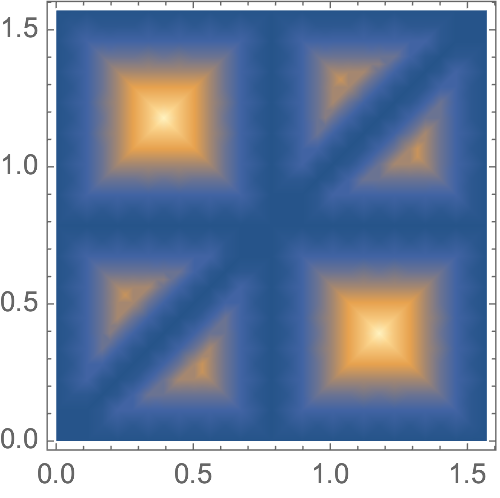
DensityPlot[f[x, y], {x, 0, π/2}, {y, 0, π/2}, PlotRange -> All, Exclusions -> None] Copy the Code

kuing

咋全部都 2x 或 2y，这系数 2 不是明显多余嘛，下面直接省去了喔。

记原式为 `m`，则有 `m\leqslant1-\cos x` 且 `m\leqslant1+\cos x`，因此有 `m\leqslant1-\abs{\cos x}`，同理有 `m\leqslant1-\abs{\sin x}`，显然 `m` 非负，所以可以两式相乘得
\begin{align*}
m^2&\leqslant(1-\abs{\sin x})(1-\abs{\cos x})\\
&=1-\abs{\sin x}-\abs{\cos x}+\abs{\sin x\cos x}\\
&=1-\sqrt{1+2t}+t,
\end{align*}
其中 `t=\abs{\sin x\cos x}\in[0,1/2]`，易知上式关于 `t` 递增，所以
\[1-\sqrt{1+2t}+t\leqslant\frac32-\sqrt2\riff m\leqslant\sqrt{\frac32-\sqrt2}=1-\frac1{\sqrt2},\]
最后再取一例子说明 `m` 能取到上式的右边，就是 `x=45\du`, `y=135\du`。

（也幸亏没有 `1\pm\sin(x-y)` 什么的，不然就取不到了）

hbghlyj

将三角函数换为多项式：

1. Maximize[{Min[1, 1 - cx, 1 + cx, 1 - cx*cy - sx*sy, 1 + cx*cy + sx*sy,
2. 1 - cy, 1 + cy, 1 - sx, 1 + sx, 1 - sy, 1 + sy],
3. sx^2 + cx^2 == 1 && sy^2 + cy^2 == 1}, {sx, cx, sy, cy}]

Copy the Code

{1 - 1/Sqrt[2], {sx -> -(1/Sqrt[2]), cx -> 1/Sqrt[2], sy -> -(1/Sqrt[2]), cy -> -(1/Sqrt[2])}}